Euclidean Distance In 'n'-Dimensional Space
Euclidean distance is a measure of the true straight line distance between two points in Euclidean space.
One Dimension
In an example where there is only 1 variable describing each cell (or case) there is only 1 Dimensional space. The Euclidean distance between 2 cells would be the simple arithmetic difference: xcell1 - xcell2 (eg. APHWcell1 = 1.11603 ms and APHWcell10 = 0.97034 ms; they are (1.11603 - 0.97034) = 0.14569 ms apart).
Two Dimensions
This has already been described here.
Three Dimensions
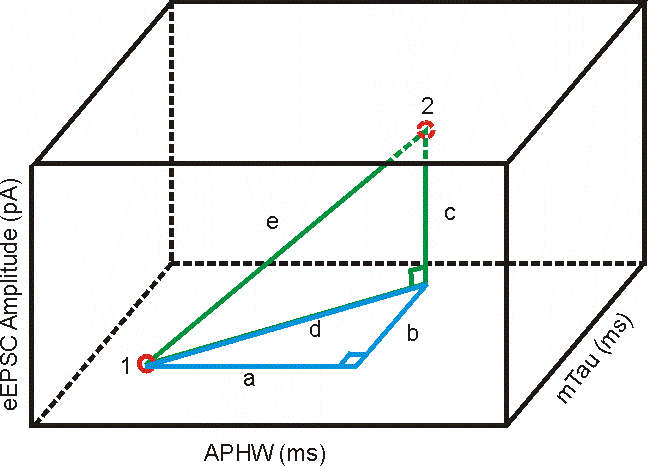
With 3 variables the distance can be visualized in 3D space such as that seen below.

Distance 'e' would be the distance between cell 1 & cell 2. We could determine it using Pythagora's theorem as seen previously, but we first need to find the value of 'd' using values 'a' and 'b'.
1. a = APHWcell1 - APHWcell2
2. b = mTaucell1 - mTaucell2
3. d2 = a2 + b2 and
4. c = eEPSCcell1 - eEPSCcell2
5. and e2 = d2 + c2
substituting a2 + b2 for c2 from line 3 you get
6. e2 = a2 + b2 + c2
substituting the values for 'a', 'b' & 'c' from 1, 2 & 4
7. e2 = (APHWcell1 - APHWcell2)2 + (mTaucell1 - mTaucell2)2 + (eEPSCcell1 - eEPSCcell2)2
This way each of the dimensions (APHW, mTau & eEPSC amplitude) are added together to get the Euclidean distance in one equation.
More Than 3 Dimensions ('n'-dimensions)
While pretty much impossible to visualize Pythagora's principle can be applied to more than 3 dimensions.
To generalize this we could say that 'e', seen above, is the distance 'D' between any 2 cells (cell i and cell j): Dij.
The number of dimensions being worked in depends on the number of variables each cell (case) is described by. If each cell is described by 3 variables then it is 3D space, if there are 20 variables then it is 20D space. Therefore 'n' variables is represented in 'n'-dimensional space. Each cell (case) will have a value 'x' for each variable (the variables will be represented from the first 'v' = 1 to the last 'v' = 'n' so that 'v' = 1 to 'n'). So distance in each dimension (like in 1, 2 & 4 above) could be represented by:
xvi - xvj which in English would be: The value of vth variable for cell i minus the value of the vth variable for cell j.
Using this:
![]()
Which, remembering Pythagora's Theorem in English: The square of the hypotenuse is equal to the sum of the squares of the other two sides. (perfectly nerdy Pythagora's joke here), itself in English would be: The square of the Distance between 2 cells (i & j; Dij) is equal to the sum (S), from the first variable (v = 1) to the last variable (n), of the squares of the distances in each dimension (which is found by finding the differences for each cell's value for each variable (cell i's value for the vth variable being xvi and cell j's value being xvj)).