Forming Clusters

At this point the decision is how to continue joining cells into clusters. At the first step it seems rather obvious; that the cells that are closest together in space are the most similar or that the cells farthest apart are the most dissimilar. Once 2 cells have been clustered together however, distance measures can be computed in a variety of ways.

Clustering Algorithms

Choosing a clustering algorithm is not that simple, partly because of the wide array that are available. Here are 5 agglomerative clustering procedures that differ in how the distance between clusters is computed.

Single Linkage (or Nearest Neighbor)

Finds the shortest distance between 2 cases and joins those 2 cases into the 1st cluster. The next shortest distance between 2 cases is then found and either it joins the first cluster, or a new cluster with 2 cases is formed. Here all cases are singly linked which makes this not a particularly good choice for clustering as long snakelike chains can form.

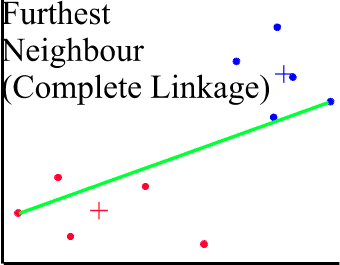
Complete Linkage (or Furthest Neighbor)

In this method clustering is based on maximum distance. All cases are completely linked within a circle of maximum diameter. Works much better by looking at the most dissimilar pairs and avoids the problem of chaining.

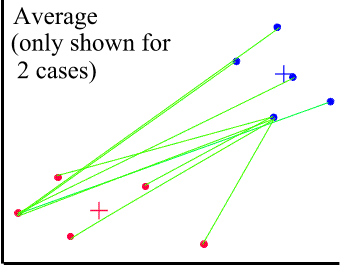
Average Linkage (or Between Groups Linkage)

Works similar to single or complete linkage, however once clusters with 2 or more cases have been formed the distance between clusters is based off of the average distance between all cases in cluster to all cases in another (as opposed to the single closest or furthest pair).

Ward's Method (Minimum Variance)

The distance here is the error sum of squares (SSE) between the 2 clusters over all of the variables. At each stage in the clustering procedure, the within cluster SSE is minimized over all partitions obtainable by combining 2 clusters from the previous stage. To see the original paper by J. H. Ward click here.

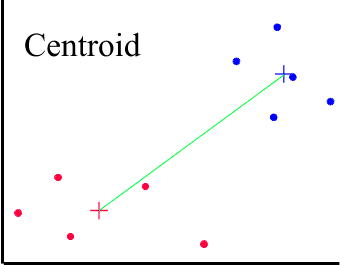
Centroid Method

The centroid method uses the controid (center of the group of cases) to determine the average distance between clusters of cases.