Error Sum of Squares

Error Sum of Squares (SSE)

SSE is the sum of the squared differences between each observation and its group's mean. It can be used as a measure of variation within a cluster. If all cases within a cluster are identical the SSE would then be equal to 0.

The formula for SSE is:

Where n is the number of observations x_i is the value of the ith observation and 0 is the mean of all the observations. This can also be rearranged to be written as seen in J.H. Ward's paper.

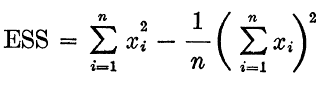
At each stage of cluster analysis the total SSE is minimized with SSE_total = SSE₁ + SSE₂ + SSE₃ + SSE₄ .... + SSE_n. At the initial stage when each case is its own cluster this of course will be 0.

You can stop reading right here if you are not interested in the mathematical treatment of this in Ward's method. It's really not important in getting Ward's method to work in SPSS.

Used in Ward's Method of clustering in the first stage of clustering only the first 2 cells clustered together would increase SSE_total. For cells described by more than 1 variable this gets a little hairy to figure out, it's a good thing we have computer programs to do this for us. If you are interested in trying to make your own program to perform this procedure I've scoured the internet to find a nice procedure to figure this out. The best I could do is this: when a new cluster is formed, say between clusters i & j the new distance between this cluster and another cluster (k) can be calculated using this formula:

d_k.ij = {(c_k + c_i)d_ki + (c_j + c_k)d_jk − c_kd_ij}/(c_k + c_i + c_j).

Where d_k.ij = the new distance between clusters, c_i,j,k = the number of cells in cluster i, j or k; d_ki = the distance between cluster k and i at the previous stage.

Back at the first stage (the zero^th stage being individual cells) this means that the two closest cells in terms of (usually) squared Euclidean distance will be combined. The SSE will be determined by first calculating the mean for each variable in the new cluster (consisting of 2 cells). The means of each of the variables is the new cluster center. The 'error' from each point to this center is then determined and added together (equation 1).

Remember that distance in 'n' dimensions is:

D_ij = distance between cell i and cell j; x_vi = value of variable v for cell i; etc.

Squared Euclidean distance is the same equation, just without the squaring on the left hand side:

This of course looks a lot like equation 1, and in many ways is the same. However, instead of determining the distance between 2 cells (i & j) its between cell i (or j) and the vector means of cells i & j.

So, the SSE for stage 1 is:

Sorry, about using the same variable (x) for 2 different things in the same equation. This will determine the distance for each of cell i's variables (v) from each of the mean vectors variable (x_vx) and add it to the same for cell j. This is actually the same as saying equation 5 divided by 2 to give:

The '2' is there because it's an average of '2' cells.

This is just for the first stage because all other SSE's are going to be 0 and the SSE at stage 1 = equation 7. For the example data used in this website cells 2 & 19 are joined in the first stage giving an SSE value of 0.278797. This cluster is never going to be broken apart again for the rest of the stages of clustering, only single cells or cells in other clusters may join with it.

Continuing in the example; at stage 2 cells 8 &17 are joined because they are the next closest giving an SSE of 0.458942. Because all SSE's have to be added together at each stage the total SSE₂ is going to be 0.737739 (you'll find the same numbers doing the equations in Excel or using Ward's Method hierarchical cluster analysis in SPSS). At the 3^rd stage cells 7 & 15 are joined together with a SSE of 0.549566. This again has to be added giving a total SSE₃ of 1.287305.

At the 4^th stage something different happens. Cell 3 combines with cells 8 & 17 (which were already joined at stage 3). Equation 5 can't be used in this case because that would be like treating the cluster with cells 8 & 17 in it as a single point with no error (SSE) associated with it. This is why equation 3 has to be used. For the purposes of Ward's Method d_k.ij is going to be the same as SSE because it is being divided by the total number cells in all clusters to obtain the average (c_k + c_i + c_j; the same as dividing by '2' cells in equation 7). I've calculated this on this Excel spreadsheet here. So d_k.ij is 0.573716.

Now there are these clusters at stage 4 (the rest are single cells and don't contribute to the SSE):

1. (2 & 19) from stage 1; SSE = 0.278797

2. (8 & 17) from stage 2; SSE = 0.458942

2. (7 & 15) from stage 3; SSE = 0.549566

3. ((8 &17) & 3) from stage 4; SSE = 0.573716

Adding all of these up results in SSE₄ = 1.861021

Equation 3 can be used at all stages it's just that with only 2 cells being joined it is reduced to equation 7. This obviously becomes quite tedious doing it manually because not only do you do this addition you have to find the smallest distance at each stage which means redoing distance matrices. Good thing there are programs already made to take this tedium out of our lives. But this info should be handy if you want to make your own program.

The point of doing all of this is to not only find the nearest cluster pairs at each stage, but also to determine the increase in SSE at each stage if this is to be used for plotting dendrograms or determining cutoff points for the number of clusters.