Determining The Right Number Of Clusters
This is a somewhat arbitrary procedure; one of the weakest aspects of performing cluster analysis. Here you have to figure out how many clusters you want to work with and how you want to do this. There are different methods (stopping rules) in doing this, usually involving either some measure of dis/similarity (distance) between clusters or to adapt statistical rules or tests to determine the right number of clusters.
One method that works fairly well (although tends to underestimate the actual number of clusters) is to look at the within cluster similarity at each stage. This was introduced rather amusingly in 1953 by R. L. Thorndike (Psychometrika, 18[4]; 267-276), and although in that treatise he didn't think he was that successful in determining a way to get at the right number of clusters the "Thorndike" method is used widely nonetheless.

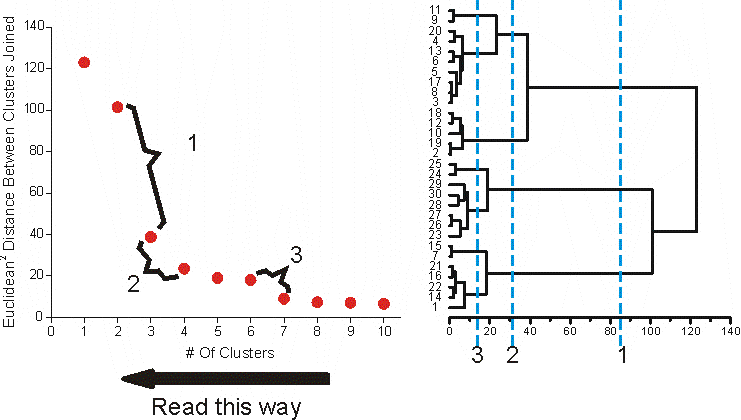
Here the increase in SSE as clusters are joined (the same as the squared Euclidean distance between clusters). It is rather odd to look at the graph this way because this is hierarchical clustering it is better to read from the right to left rather than vice versa.
The largest ΔSSE is between having 3 clusters or 2 clusters (point 1 on graph), indicating that 3 clusters divides the cells into much more homogenous groups than does 2 groups. From this reasoning it could be possible to pick 3 clusters as the final solution.
There are indications at 2 & 3 that these may also be good places to 'stop' the clustering. Either at 4 clusters or 7 clusters. It could also be that these indicate spots where there are sub-clusters of the 3 clusters at point 1.
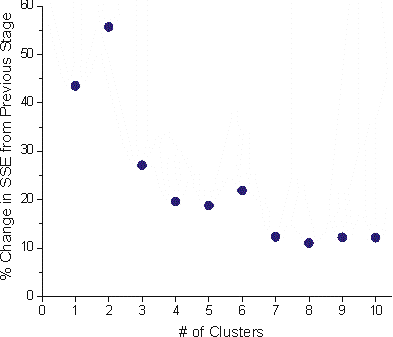
Another method is to look at the % increase in SSE (or whatever clustering coefficient is used, remember in Ward's method it is SSE) at each subsequent stage of clustering. It can be seen here as well there is a big change from 7 to 6, 4 to 3 and 3 to 2. So you could say there are 7, 4 or 3 potential clusters.